ipv4:216.73.216.164
Année scolaire 2025-2026

Exponentielle
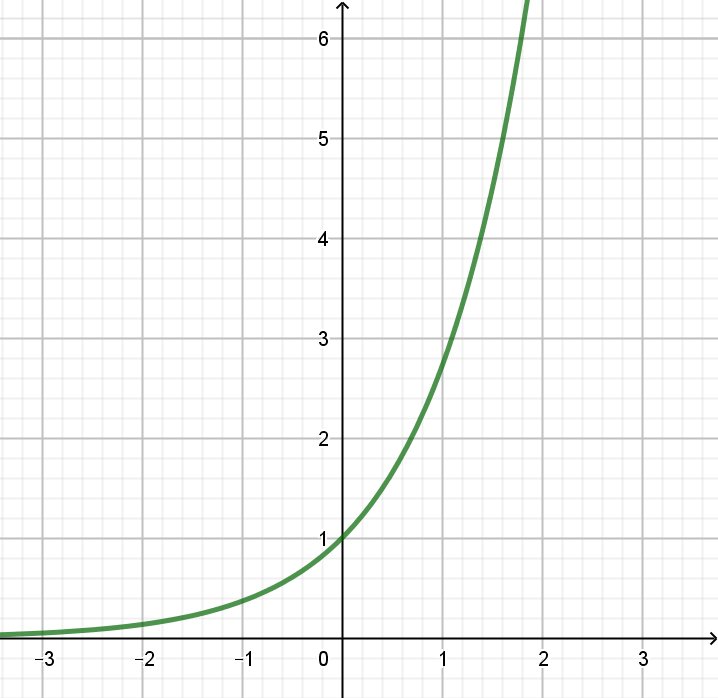
- Définition de l'exponentielle
- Le problème différentiel $y'(x) = y(x)$ et $y(0) = 1$
- Une solution existe
- elle est unique
- Propriétés
- étude de $f(x) = exp(x)\times exp(-x)$
- Variations: $exp$ est continue, ne s'annule pas et vaut 1 en 0
- Limites en + et - $\infty$ : étude de $f(x) = exp(x)-(1+x)$
- Tableau de variation avec le nombre $e$
- Propriétés algébriques
- $exp(a+b)$ : étude de $f(x) = exp(x+y)/exp(x)$ et $f(0)$
- $exp(-a)$, $exp(a-b)$
- La notation $e^x$
- Limites
- $\lim\limits_{x\to+\infty} e^x$ et $\lim\limits_{x\to-\infty} e^x$
- $\lim\limits_{x\to+\infty} \dfrac{e^x}{x^n}$ et $\lim\limits_{x\to-\infty} x^n e^x$ pour $n$ quelconque
écrit par : Stéphane Le Méteil, le 16/11/2025
Version du 30 Janvier 2026