haut ⇨ ⇦bas
Cira1
ipv4:216.73.216.164
Année scolaire 2025-2026
stylo
Programme

Le référentiel du BTS Contrôle industriel et régulation automatique est disponible : ici

La partie qui nous intéresse commence à la page 105 pour la répartition des modules et la page 43 du document annexe propose des aménagements.

La réussite à l'épreuve de BTS est sanctionnée en contrôle en cours de formation (CCF) sous la forme de deux situations de 55 minutes comme le stipule le BO n°13 du 31 mars 2016.

La première situation permet l’évaluation, par sondage, des contenus et des capacités associés aux modules du programme de mathématiques suivants:

  • Nombres complexes.
  • Fonctions d’une variable réelle.
  • Fonctions d’une variable réelle et modélisation du signal.
  • Calcul intégral.
  • Équations différentielles.

Horaires minimaux de mathématiques: 2 + 1 en première année, 1 + 1 en seconde année.

écrit par : Stéphane Le Méteil, le 01/09/2025
Bases de calcul



  1. Calculs fractionnaires
  2. Développer et factoriser
  3. Puissances
  4. Équations
  5. Généralités sur les fonctions
  6. Fonctions affines
  7. Statistiques
  8. Probabilités
  9. Arithmétique
écrit par : Stéphane Le Méteil, le 02/09/2025
Fonctions affines
Systèmes :
Automates
  1. Définitions
    1. fonction affine, linéaire, constante
    2. calculer une image, calculer un antécédent
    3. déterminer une fonction
  2. Représentation graphique
    1. rappels sur le vocabulaire : abscisses, ordonnées, repère orthonormé, graphe de fonction
    2. dessiner la représentation graphique
    3. coefficient directeur et ordonnées à l'origine
    4. lire ou calculer le coefficient directeur, l'ordonnée à l'origine
  3. Résolution de l'équation $ax+b=0$
  4. Sens de variation de $f(x) = ax+b$
  5. Signe de $f(x) = ax+b$
  6. Systèmes de deux équations à deux inconnues
écrit par : Stéphane Le Méteil, le 06/09/2025
Minitests N°1 et 2

Minitest 1 tex Corrigé tex : calculs basiques et fonctions affines

Minitest 2 tex Corrigé tex : calculs, fonctions affines, signe de produits
écrit par : Stéphane Le Méteil, le 13/09/2025
Second degré


icone
  1. Définitions
    1. Définition : fonction du 2nd degré
    2. Savoir lire $a$, $b$ et $c$
  2. Formes canoniques
    1. Sur un exemple
    2. Démonstration
    3. Notations $\alpha$, $\beta$ et $\Delta$
    4. Interprétation graphique
  3. Factorisation
    1. A partir de la forme canonique
    2. Avec le discriminant
  4. Résolution de l'équation
    1. Lorsque $\Delta < 0$
    2. Lorsque $\Delta = 0$
    3. Lorsque $\Delta > 0$
    4. Interprétation graphique
  5. Signe du trinome
    1. Lorsque $\Delta < 0$
    2. Lorsque $\Delta = 0$
    3. Lorsque $\Delta > 0$
  6. Représentation graphique
    1. Lorsque $\Delta < 0$ avec a > 0, avec a < 0
    2. Lorsque $\Delta = 0$ avec a > 0, avec a < 0
    3. Lorsque $\Delta > 0$ avec a > 0, avec a < 0
▲
écrit par : Stéphane Le Méteil, le 22/09/2025
Minitest N°3

Minitest 3 tex Corrigé tex : fonctions affines et début du second degré
écrit par : Stéphane Le Méteil, le 27/09/2025
Contrôles N°1 et 1bis

Contrôle N°1 Enoncé. tex Corrigé tex Fonctions affines et fonctions du second degré.
Contrôle N°1bis Enoncé. tex Corrigé tex Fonctions du second degré.
écrit par : Stéphane Le Méteil, le 30/09/2025
Dérivation

icone
  1. Définitions
    1. repères
    2. abscisses ordonnées, coordonnées
    3. représentation graphique
    4. taux d'accroissement
    5. corde et tangente
  2. Nombre dérivé
    1. Définition
    2. Equation de tangente
  3. Fonction dérivée
    1. Définition
    2. Dérivées des fonctions usuelles
    3. Dérivées et opérations
  4. Applications de la dérivée
    1. Variation de fonction
    2. Recherche d'extrema
écrit par : Stéphane Le Méteil, le 02/11/2025
Minitest N°4

Minitest 4 tex Corrigé tex : second degré et nombre dérivé
écrit par : Stéphane Le Méteil, le 05/11/2025
Exponentielle
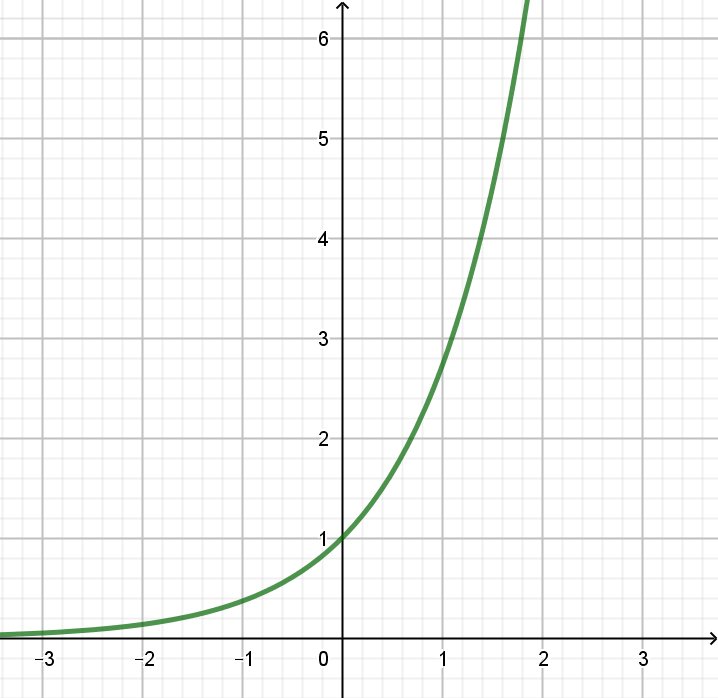
courbe de la fonction exponentielle icone
  1. Définition de l'exponentielle
    1. Le problème différentiel $y'(x) = y(x)$ et $y(0) = 1$
    2. Une solution existe
    3. elle est unique
  2. Propriétés
    1. étude de $f(x) = exp(x)\times exp(-x)$
    2. Variations: $exp$ est continue, ne s'annule pas et vaut 1 en 0
    3. Limites en + et - $\infty$ : étude de $f(x) = exp(x)-(1+x)$
    4. Tableau de variation avec le nombre $e$
  3. Propriétés algébriques
    1. $exp(a+b)$ : étude de $f(x) = exp(x+y)/exp(x)$ et $f(0)$
    2. $exp(-a)$, $exp(a-b)$
    3. La notation $e^x$
  4. Limites
    1. $\lim\limits_{x\to+\infty} e^x$ et $\lim\limits_{x\to-\infty} e^x$
    2. $\lim\limits_{x\to+\infty} \dfrac{e^x}{x^n}$ et $\lim\limits_{x\to-\infty} x^n e^x$ pour $n$ quelconque
écrit par : Stéphane Le Méteil, le 16/11/2025
Minitest N°5

Minitest 5 tex (Corrigé = le cours) : les bases sur l'exponentielle
écrit par : Stéphane Le Méteil, le 25/11/2025
Contrôle N°2

Contrôle N°2 Enoncé. tex Corrigé tex Fonctions affines, du second degré, exponentielle et notions autour de la dérivation.
écrit par : Stéphane Le Méteil, le 02/12/2025
Logarithme népérien
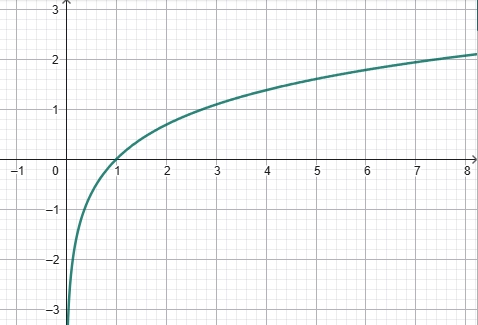
courbe de la fonction logarithme népérien
  1. Définition
    1. CTVI avec $exp(x) = k$
    2. Définition de $\ln(k)$
    3. Définition de la fonction $\ln$
    4. Courbe représentative
    5. Pour tout $x\in I\!\!R$ et $y\in I\!\!R^+_*$ on a :
      $y=e^x$ ssi $x= \ln(y)$
  2. Propriétés algébriques
    $ \ln(a\times b) $ $ \ln(a^n) $ $ \ln(\frac1a) $ $ \ln(\frac{a}{b}) $
  3. Etude de la fonction ln
    1. Ensemble de définition
    2. Dérivée et variations
    3. Limites et croissances comparées
    4. Courbe et fiche mémoire
  4. Log
    1. Définition
    2. Quelques formules
    3. Intérêt
écrit par : Stéphane Le Méteil, le 08/12/2025
Complexes
icone icone
  1. Généralités
    • définition, notation algébrique,ensemble $C$
    • partie réelle, partie imaginaire, imaginaire pur
  2. Opérations sur les complexes
    • ajouter, soustraire mutiplier, élèver à une puissance
    • conjuguer
    • inverser diviser
  3. Equations du second degré
    • $ \Delta > 0$
    • $ \Delta = 0$
    • $ \Delta < 0$
  4. Représentations des complexes
    • affixe et point image, vecteur image
    • axe des réels, des imaginaires purs
  5. Modules et arguments
    1. Modules
      1. définition comme une distance
      2. modules et opérations
    2. Arguments de $z\neq 0$
      1. définition
      2. rappels de trigo : sohcahtoa, valeurs remarquables
      3. méthodes pour calculer un argument
        • cos/sin
        • tan
        • calculatrice
      4. arguments et opérations
  6. Autres notations
    1. Polaire
    2. Trigonométrique
    3. Exponentielle
▲
écrit par : Stéphane Le Méteil, le 05/01/2026
Minitests N°6 et 7

Minitest 6 tex Corrigé tex : les bases sur les complexes
Minitest 7 tex Corrigé tex : modules et arguments
écrit par : Stéphane Le Méteil, le 14/01/2026
Primitives
icone
  1. Dérivées usuelles
    1. polynômes
    2. exponentielles
    3. logarithmes
    4. inverses
    5. produits
    6. quotients
    7. puissances
    8. racines carrées
    9. trigonométriques
  2. Primitives simples
    1. définition d'une primitive ?
    2. qu'appelle-t-on 'intégrer' ?
    3. polynômes
    4. exponentielles
    5. inverses
    6. compositions simples
 
▲
écrit par : Stéphane Le Méteil, le 03/02/2026
Derniers articles publiés :
Le 13/02/2026 dans bia sous le titre : 13 Février
Le 09/02/2026 dans bia sous le titre : 6 Février
Le 03/02/2026 dans Cira1 sous le titre : Primitives
Le 03/02/2026 dans Première sous le titre : Contrôle N°5
Le 01/02/2026 dans Latex sous le titre : Bonne entête
Version du 30 Janvier 2026