haut ⇨ ⇦bas
Terminale
ipv4:216.73.216.164
Année scolaire 2025-2026
stylo
Programme
Le programme officiel

Conseils pour l'année
écrit par : Stéphane Le Méteil, le 01/09/2025
Suites numériques

suites et ti suites et casio suites et numworks Feuilles d'exercices

Automates
  1. Définitions
    1. implicite
    2. explicite
    3. récursive
    vocabulaire (indice/rang/numéro, terme général, suite)
    notation (écriture), précédent, suivant
    utilisation de la calculatrice pour calculer des termes
  2. Deux types de base
    1. arithmétique
    2. géométrique
    exemples, contre exemple
  3. Vocabulaire et méthodes
    1. croissante
    2. décroissante
    3. majorée
    4. minorée
    5. bornée
    6. méthode pour étudier les variations
  4. Récurence
    1. principe
    2. exemples, inégalité de Bernoulli

dominos pour illustrer la récurrence
écrit par : Stéphane Le Méteil, le 05/09/2025
Minitests

Minitest 1 tex Corrigé tex : bases sur les suites
Minitest 2 tex Corrigé tex : récurrences
Minitest 3 tex Corrigé tex : récurrences
Minitest 4 tex Corrigé tex : récurrence, formes indéterminées et limite
Minitest 5 tex Corrigé : exponentielle et logarithme
Minitest 6 tex Corrigé tex : base de combinatoire / dénombrement
Minitest 7 tex Corrigé tex : base de combinatoire / dénombrement (bis)
Minitest 8 tex Corrigé tex : équation différentielle
Minitest 9 tex Corrigé tex : début géométrie dans l'espace
écrit par : Stéphane Le Méteil, le 12/09/2025
Limite de suites


  1. convergence
    1. définition avec les intervalles
    2. suites de référence
    3. opération sur les limites
  2. divergences
    1. diverger vers un infini
    2. diverger sans limite
    3. opération sur les limites, formes indéterminées
  3. Le cas des suites géométriques
    1. $q > +\infty $
    2. $ -1 < q < 1$
    3. $ 1 < q $
    4. $ q =0 $ ou $ 1 $ ou $-1 $
  4. Méthodes et outils
    1. Critères de comparaison
    2. Théorème des Gendarmes
    3. Théorème des suites monotones bornées
▲
écrit par : Stéphane Le Méteil, le 22/09/2025
Contrôle N°1
Enoncé. tex
Corrigé. tex
  • généralités sur les suites
  • récurrence
  • tout début des limites.
▲
écrit par : Stéphane Le Méteil, le 29/09/2025
Limites de fontions

Révisions :
  1. Limites à l'infini
    1. limite infinie
    2. limite finie et asymptote horizontale
  2. Limites en un nombre a
    1. infinie et asymptote verticale
    2. limite finie
  3. Opérations sur les limites
    1. les cas triviaux
    2. les formes indéterminées
  4. Limites et comparaison
    1. $ f(x) > g(x) $
    2. $ f(x) < g(x) $
    3. $ g(x) < f(x) < h(x) $
écrit par : Stéphane Le Méteil, le 09/10/2025
Devoir libre

Enoncé. tex
Corrigé. tex
  • généralités sur les suites
  • suites géométriques
  • suites arithmético-géométriques
  • somme de termes d'une suite
  • limites de suites
  • récurrence
écrit par : Stéphane Le Méteil, le 13/10/2025
Contrôle N°2

Enoncé. tex
corrigé tex
  • généralités sur les suites
  • suites géométriques
  • suites arithmético-géométriques
  • somme de termes d'une suite
  • limites de suites
  • récurrence
▲
écrit par : Stéphane Le Méteil, le 28/10/2025
Continuité

  1. Continuité en a
    1. Définition
    2. Exemples simples
    3. Fonctions définies par morceaux
  2. Continuité sur un intervalle I
    1. Définition
    2. Graphiquement
    3. Exemples de fonctions continues
  3. Opérations et continuité
    1. Additions, soustractions, multiplications, multiples
    2. Inverse : le cas des valeurs interdites, exemple
    3. Exercice d'application
    4. Composition
  4. Les théorèmes TVI et CTVI
    1. TVI : énoncé, usage avec $ f(x) = k $
    2. CTVI : énoncé, usage avec $ f(x) = k $ avec $ f(x) = 0$
  5. Application aux suites
    1. Limite et continuité
    2. Convergence
écrit par : Stéphane Le Méteil, le 02/11/2025
Logarithme népérien

Révisions :
  1. Rappels sur l'exponentielle
    • voir ci-contre
  2. Définition
    1. CTVI avec $exp(x) = k$
    2. Définition de $\ln(k)$
    3. Définition de la fonction $\ln$
    4. Courbe représentative
    5. Pour tout $x\in I\!\!R$ et $y\in I\!\!R^+_*$ on a :
      $y=e^x$ ssi $x= \ln(y)$
  3. Propriétés algébriques
    $ \ln(a\times b) $ $ \ln(a^n) $ $ \ln(\frac1a) $ $ \ln(\frac{a}{b}) $
  4. Etude de la fonction ln
    1. Ensemble de définition
    2. Dérivée et variations
    3. Limites et croissances comparées
    4. Courbe et fiche mémoire
  5. Log
    1. Définition
    2. Quelques formules
    3. Intérêt
écrit par : Stéphane Le Méteil, le 16/11/2025
Contrôle N°3

Enoncé. tex
corrigé tex
  • suites arithmético-géométriques
  • limites de suites
  • récurrence
  • théorème CTVI, suites monotones
  • fonction à base d'exp, limites, variations, asymptote, extremum
  • fonction à base de ln, limites, variations, asymptote, extremum
▲
écrit par : Stéphane Le Méteil, le 01/12/2025
Probabilités

Probabilités conditionnelles. Variables aléatoires
  1. Rappels et compléments
    1. définitions : expérience aléatoire, issue, univers, événement élémentaire, événement certain, événement impossible, intersection, réunion, contraire, incompatibles
    2. propriétés, partition (SCE)
    3. définir une probabilité, loi de proba, équiprobabilité, cardinal
    4. propriétés : proba d'un événement, proba d'une réunion, proba du contraire
    5. probabilités conditionnelles : définition, formule des probabilités totales, généralisation à un S.C.E.
    6. représentation sous la forme d'arbre : placer $P_A(B)$
  2. Variables aléatoires
    1. définition : une règle du jeu, associer un nombre à toute issue d'une expérience aléatoire
    2. loi de probabilité : donner la liste des différents $x_i$ avec leurs $p_i$
    3. espérance : la somme des $x_ip_i$, interprétation
    4. variance définition et formule de Huygens
    5. écart-type : définition
▲
écrit par : Stéphane Le Méteil, le 08/12/2025
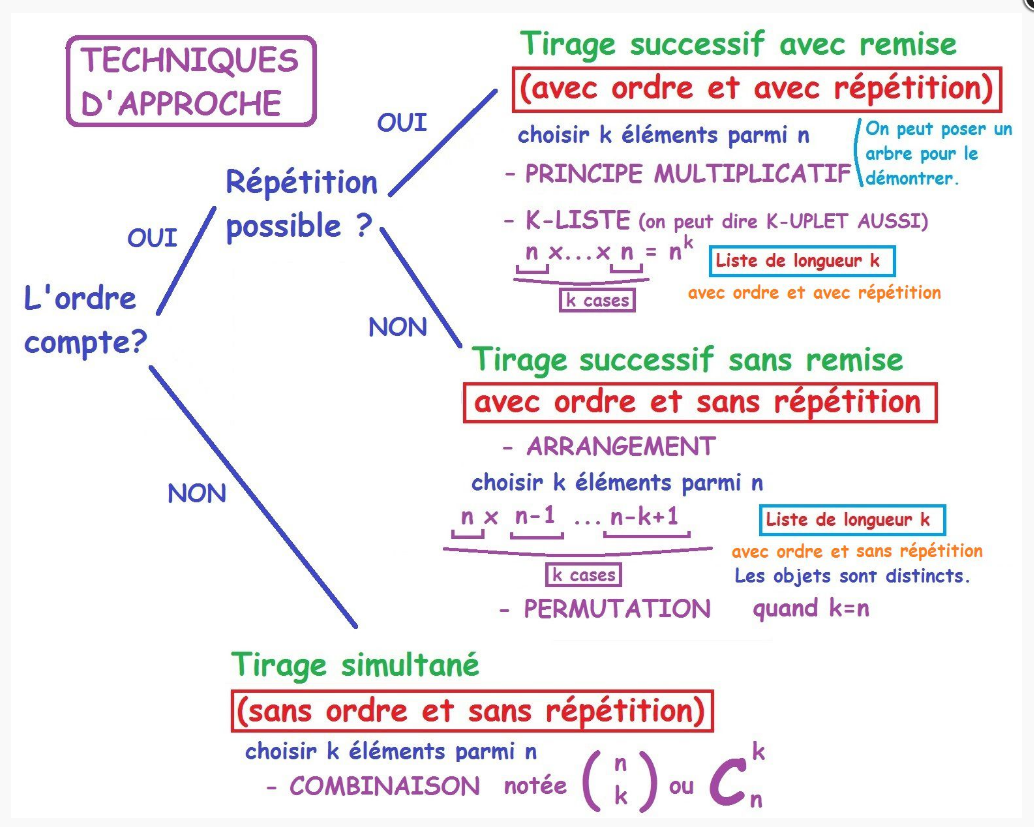
Dénombrement
les différentes possibilités de listes
  1. Principes additif et multiplicatif
    1. Cardinal d'un ensemble fini
    2. Cardinal de $E\cup F$ avec $E\cap F = \emptyset$, principe additif
    3. p-uplet : définition, exemple, contre-exemple
    4. produit cartésien : définition, représentation
    5. Cardinal de $E\times F$, principe multiplicatif
  2. Arrangements et permutations
    1. Factoriel : définitions et propriétés
    2. Arrangements : définition, exemple, nombre d'arrangements, notation
    3. Permutation : définition, exemple, notation
  3. Combinaisons
    1. Définition, exemple
    2. Nombre de combinaisons, notation, propriétés
▲
écrit par : Stéphane Le Méteil, le 15/12/2025
Révisions

Toutes ces vacances, je vous ai proposé un exercice pour réviser doucement.

Etudes de fonctions tex

écrit par : Stéphane Le Méteil, le 03/01/2026
Contrôle N°4

Enoncé. tex
Corrigé tex
Second degré.
  • probabilité conditionnelle
  • variable aléatoire, espérance, variance
  • suite, récurrence, algorithme
  • suite géométrique
  • logarithme népérien
  • limites, dérivée, variation, ctvi
▲
écrit par : Stéphane Le Méteil, le 08/01/2026
Primitives et équa. diff.
icone icone
  1. Primitives
    1. définitions et 1ères propriétés
      • primitive, existences, multiplicité
    2. primitives usuelles
    3. primitives et opérations
  2. Equations différentielles
    1. définition
    2. résoudre une équation différentielle
    3. sur un exemple : deux présentations
▲
écrit par : Stéphane Le Méteil, le 22/01/2026
Géométrie 3D
icone icone
  1. Les droites dans l'espace
    1. coordonnées d'un point, d'un vecteur
    2. opérations sur les vecteurs
    3. colinérité, vecteur directeur de droite
    4. équations paramétriques de droites
    5. positions relatives de deux droites
  2. Orthogonalité dans l'espace
    1. produit scalaire
    2. vecteurs orthogonaux
    3. distance entre deux points
  3. Les plans dans l'espace
    1. (non) colinéarité
    2. vecteur normal d'un plan
    3. équations de plans
    4. positions relatives de deux plans
  4. Positions relatives d'une droite et d'un plan
    1. géométriquement
    2. par le calcul
  5. Projection orthogonale
    1. géométriquement
    2. par le calcul
    3. distance point-plan, volume
▲
écrit par : Stéphane Le Méteil, le 01/02/2026
Derniers articles publiés :
Le 13/02/2026 dans bia sous le titre : 13 Février
Le 09/02/2026 dans bia sous le titre : 6 Février
Le 03/02/2026 dans Cira1 sous le titre : Primitives
Le 03/02/2026 dans Première sous le titre : Contrôle N°5
Le 01/02/2026 dans Latex sous le titre : Bonne entête
Version du 30 Janvier 2026