ipv4:216.73.216.164
Année scolaire 2025-2026

Logarithme népérien
- expo et LN
- Fiche mémoire tex
- Exercices logarithmes tex
- Exercices pratiques tex
- cours sur les logarithmes tex
- Définition
- CTVI avec $exp(x) = k$
- Définition de $\ln(k)$
- Définition de la fonction $\ln$
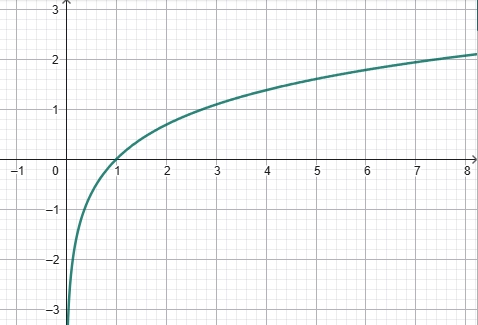
- Courbe représentative
- Pour tout $x\in I\!\!R$ et $y\in I\!\!R^+_*$ on a :
$y=e^x$ ssi $x= \ln(y)$
- Propriétés algébriques
$ \ln(a\times b) $ $ \ln(a^n) $ $ \ln(\frac1a) $ $ \ln(\frac{a}{b}) $ - Etude de la fonction ln
- Ensemble de définition
- Dérivée et variations
- Limites et croissances comparées
- Courbe et fiche mémoire
- Log
- Définition
- Quelques formules
- Intérêt
écrit par : Stéphane Le Méteil, le 08/12/2025
Version du 30 Janvier 2026